Allocation of poll observers to polling stations with networkx

I did a little bit of work recently to help the Wake county in North Carolina allocate poll observers to polling stations. One of the reasons poll observers cancel is because the polling station ends up being too far to travel. Now if we thought of this before we send them an allocation we can find an optimal allocation using one of the many matching algorithms.

If we have already sent out your assignments, we can still make your poll observers weakly better off by allowing them to trade assignments. This starts getting messy if Lián wants Rohan’s polling station, Rohan wants Tere’s polling station, and Tere wants Kwame’s, and Kwame wants Lián’s. Here we look at the Top-trading cycle, a simple algorithm with some very nice properties, that allow us to improve our allocation while making sure no one is worse off (it’s pareto improving).

You can find the (really messy) code for this here.

Let’s make up some data

I’m going to evenly scatter the polling stations and observers so it’s obvious to a human on what the optimal allocation would be.

grid_dim = 5
n_names_location = grid_dim**2

x = np.arange(grid_dim)
y = np.arange(grid_dim)
xx, yy = np.meshgrid(x, y)

even_points = np.stack([xx.ravel(), yy.ravel()]).T

observers = pd.DataFrame()
polling_station = pd.DataFrame()
past_names = []
for i in range(n_names_location):
    name = names.get_first_name()
    while name in past_names:
        name = names.get_first_name()
    past_names.append(name)
    observers = observers.append({
                                  'idx':i,
                                  'observer': name,
                                  'location': even_points[i] /1.5 + 0.75
                                 }, ignore_index=True)
    polling_station = polling_station.append({
                                              'idx':i,
                                              'polling_station': f'PollingStation_{i}',
                                              'location': even_points[i]
                                             }, ignore_index=True)

Let’s make a graph out of this and see what it looks like.

G_raw = nx.DiGraph()

for n in polling_station.assigned_observer.values:
    G_raw.add_node(n, node_type = 'observer')
for n in polling_station.polling_station.values:
    G_raw.add_node(n, node_type = 'poll_station')

# where to draw the nodes
pos = assigment.set_index('polling_station')['location_ps'].to_dict()
pos.update(assigment.set_index('assigned_observer')['location_obs'].to_dict())

Optimal Allocation

Networkx is a python library for working with graphs. It’s got a tonne of algorithms already coded up for you. This includes the Karp’s matching algorithm. Let’s use that to find the optimal matching.

To create our weighted bipartite graph, we need to compute the distance between all our observers and the polling stations.

def get_distance_df(observers, polling_station):
    """
    Given a dataset of observers and polling_stations, return a matrix od
    distances between them.

    Parameters
    ----------
    observers: pd.Dataframe
        A dataframe of observers. Should have `observer` and `location` as columns
    polling_station: pd.Dataframe
        A dataframe of polling_station. Should have `polling_station` and `location` as columns

    Returns
    -------
    distance_df: pd.Dataframe
        A dataframe of distances between all observers and polling_stations

    """

    obs_idx, poll_st_idx = np.meshgrid(np.arange(observers.shape[0]), np.arange(polling_station.shape[0]))
    distance_arr = polling_station['location'].values[poll_st_idx.ravel()] - observers['location'].values[obs_idx.ravel()]
    distance_arr = np.stack(distance_arr)

    distance_df = pd.DataFrame({'distance':np.linalg.norm(distance_arr, axis=1)})
    distance_df['observer_idx'] = obs_idx.ravel()
    distance_df['observer_name'] = observers.iloc[obs_idx.ravel()]['observer'].values
    distance_df['polling_station_idx'] = poll_st_idx.ravel()
    distance_df['polling_station'] = polling_station.iloc[poll_st_idx.ravel()]['polling_station'].values

    return distance_df

Great. Now let’s build our graph using networkx.

G_full = nx.DiGraph()
G_full.add_nodes_from(G_raw.nodes(data=True))
for x in distance_df[['polling_station', 'observer_name', 'distance']].itertuples(index = False, name=None):
    G_full.add_edge(x[1], x[0], distance = x[2])

We have added an edge between every polling station and observer. No we can use networkx to solve the matching problem and give us the ones that minimise total distance:

from networkx.algorithms.bipartite.matching import minimum_weight_full_matching

observer_nodes, _ = nx.bipartite.sets(G_full)
optimal_matching = minimum_weight_full_matching(G_full, top_nodes = observer_nodes, weight='distance')

G_optimal = nx.DiGraph()
G_optimal.add_nodes_from(G_raw.nodes(data=True))
G_optimal.add_edges_from(zip(optimal_matching.keys(),optimal_matching.values()), edge_type = 'allocated')

f = draw_allocation(G_optimal, pos, i="")

draw_allocation just renders the graph. Check out the notebook. if you really want to know how it does that. Here’s our optimal match:

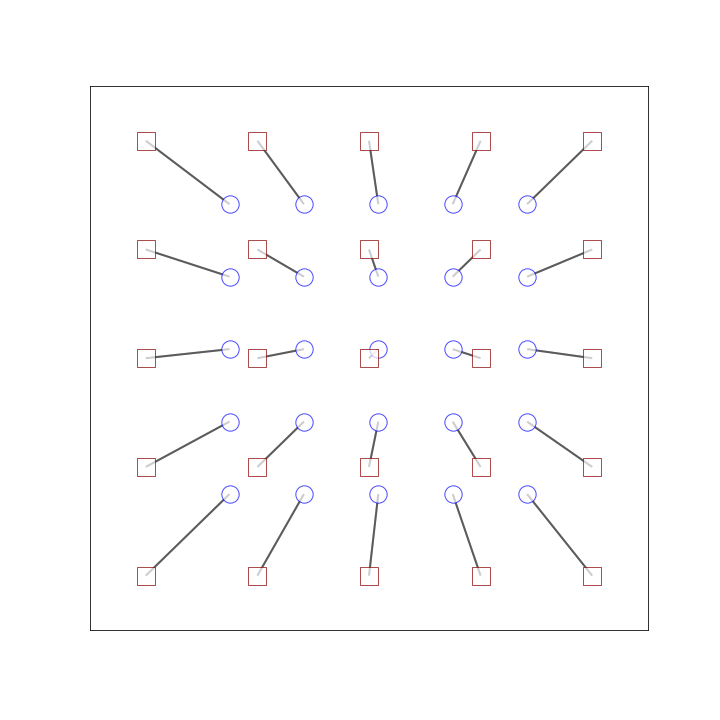
Other use cases

Pretty easy eh? There are a bunch of cases where something like this comes handy. An obvious one may be where the weight on the edges isn’t geographic distance but rather reward. You have a team of workers skilled in different things, how do you assign them to tasks to maximise reward?

Another use-case is if you are doing some sort of entity matching. You have a list of names that you want to match with another (possibly larger) list of names. You can use some metric to calculate the “distance” from each name in list 1 to every name in list 2. Setup your network with this distance as edge weights and solve for the optimal match.

Pareto-optimal reallocation

Say you have already done your allocation and you made a real hash of it because, you know, you did it in excel.

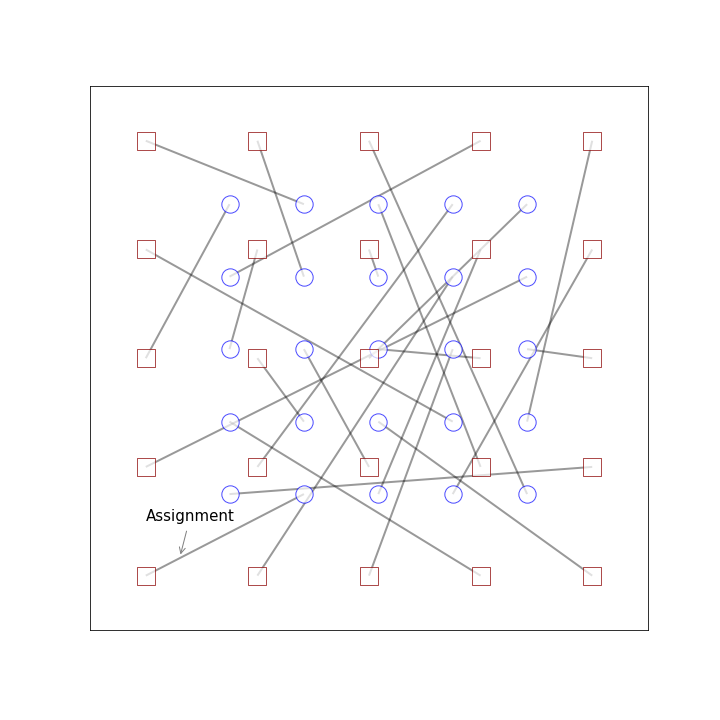
Your observers are already annoyed at you and if you make any of their travel even longer, they are sure to cancel. So we need an algorithm that makes everyone only better off and never worse. We want a Pareto improving re-allocation. The top-trading cycle, or the “House exchange” algorithm as I was taught, gives us exactly that. Here’s the algorithm from wikipedia with some minor alterations:

1. Get each observer’s “top” (most preferred) polling station. In our case, this will be the polling station closest to the observer.
2. Add an edge from each observer to their top choice of polling station.
3. Note that there must be at least one cycle in the graph (this might be a cycle of length 2, if some observer currently holds their own top polling station). Implement the trade indicated by this cycle (i.e., reallocate each polling station to the observer pointing to it), and remove all the involved observers and polling stations from the graph.
4. If there are remaining observers, go back to step 1.

It’s not a lot of code to do this:

def resolve_cycle(G, edges):
    """ Remove old edges and add new optimal ones """
    G.remove_edges_from(edges)
    new_edges = []
    for u, v in edges:
        if v.startswith("PollingStation"):
            G.add_edge(v, u, edge_type = 'allocated')
            new_edges.append((v, u))
    return G, new_edges

G_pref = build_pref(G_raw, [], distance_df)
resolved_nodes = []
all_cycles = list(nx.simple_cycles(G_pref))

while len(all_cycles) > 0:
    for cycle in nx.simple_cycles(G_pref):
        if len(cycle) == 2:
            G_pref, new_edges = resolve_cycle(G_pref, [(cycle[1], cycle[0]),(cycle[0], cycle[1])])
            if cycle[0].startswith("PollingStation"):
                poll_node, obs_node = cycle
            else:
                obs_node, poll_node = cycle
        else:
            edges = list(zip(cycle[:-1], cycle[1:])) + [(cycle[-1], cycle[0])]
            poll_nodes = [x for x in cycle if x.startswith("PollingStation")]
            obs_nodes = [x for x in cycle if not x.startswith("PollingStation")]
            G_pref, new_edges = resolve_cycle(G_pref, edges)
        resolved_nodes += cycle
    G_pref = build_pref(G_pref, resolved_nodes, distance_df)
    all_cycles = list(nx.simple_cycles(G_pref))

Here’s a series of plots showing how this works:

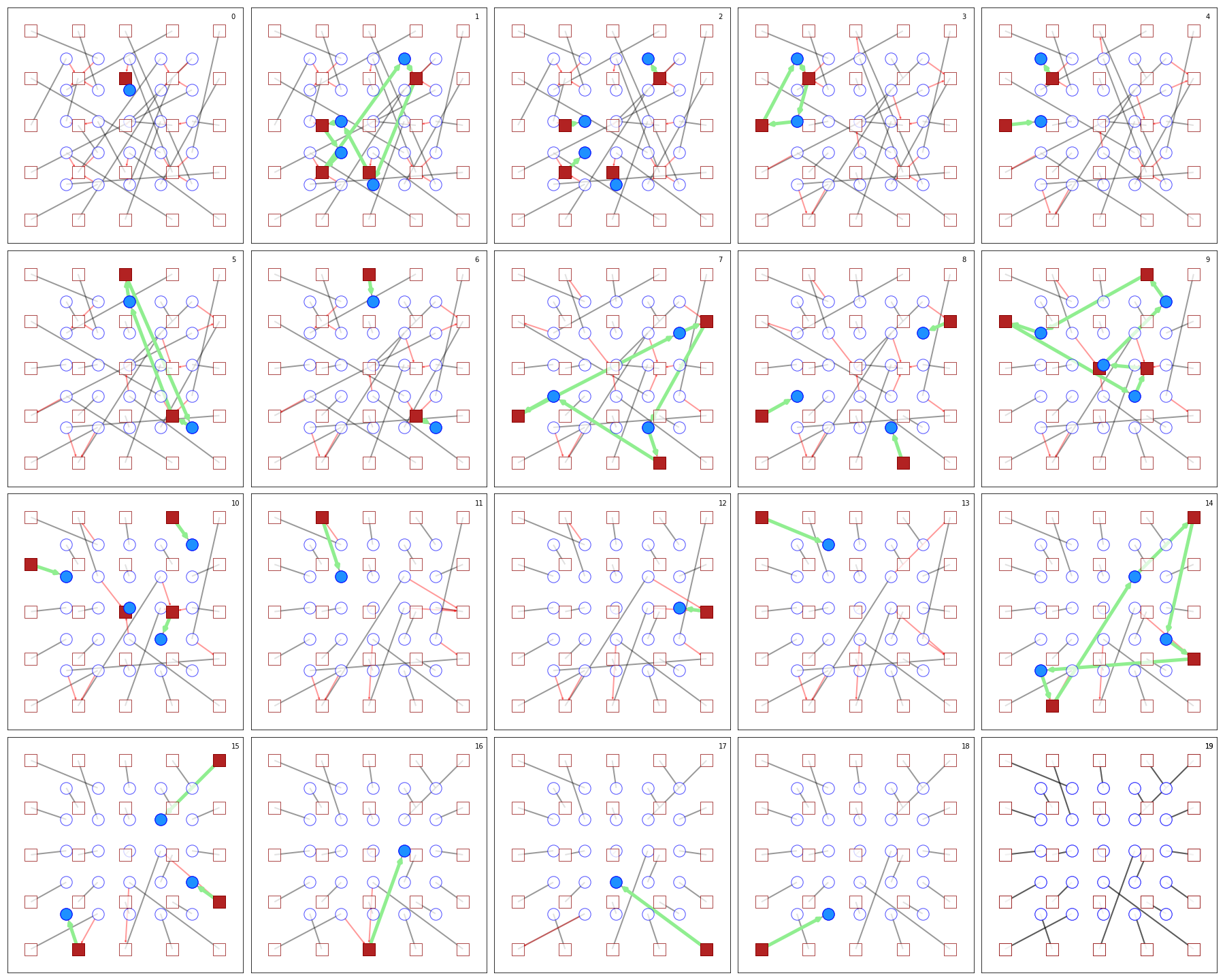
Not globally optimal but Pareto optimal

Here’s what the final allocation looks like:

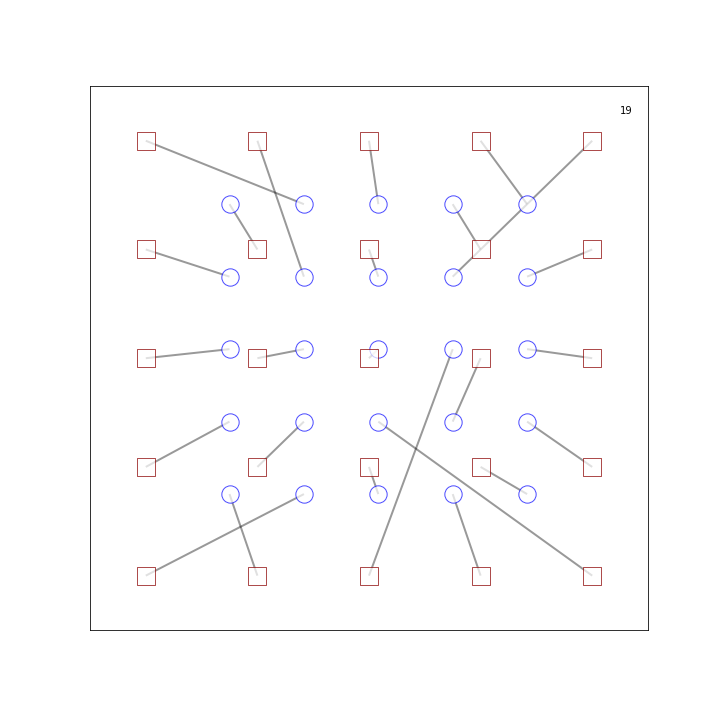
It’s a lot better than the spaghetti allocation we had at the start – but not perfect. Check out those polling stations in the bottom left. If the allocations were swapped, total distance travelled would go down but the observer on the right may be slightly worse off.

There are some nice things about this algorithm:

1. It is a truthful mechanism: If you don’t tell the truth about your preferences, you will only do worse. In our case, we are calculating the distance between the observer’s house and the polling station and using that to objectively rank their preferences. If we were to ask them to rank their preferences, it would be a bad idea for them to misrepresent it.
2. It is core stable: You can’t form a coalition (a subset of observers breaking off to do their own swapping) and do better than you would do if you stayed in the system.
3. Solution is pareto optimal: You can’t make any observer better off without making someone else worse off.

Other use cases

Extensions of this won Alvin Roth and Lloyd Shapley the Nobel prize. It has been used in many markets where the items do not have a price and but we want to allow for swapping. Kidney exchange is one such market.

I spent some time trying to adapt this to allow doctors to exchange shifts. Then life happened. Maybe I should pick that back up.